
Reverse Engineering Crypto Functions: AES
12 December 2021
By Jacob Pimental
The Advanced Encryption Standard (AES) algorithm is a successor to the Data Encryption Standard (DES). With the advancement of technology, the key length and small block size of DES made it less secure. In 1997, NIST announced a competition to come up with a stronger algorithm; thus, AES was born.
This post is a follow-up to my previous post on reverse engineering cryptographic algorithms where I provided information on the RC4 and Salsa20 algorithms. In this post, I will explain how the AES algorithm works and how you can identify it when reverse engineering an application.
Basic AES Encryption
The AES Algorithm will break up a plaintext string into 16 byte “blocks” that undergo several rounds of encryption. The steps are detailed in the official AES documentation:
- Expand provided key (Key Expansion Section)
- AddRoundKey function on the plaintext block using the expanded key
- Multiple encryption Rounds
- SubBytes function on block
- ShiftRows function on block
- MixColumns function on block
- AddRoundKey function
- Final SubBytes call
- Final ShiftRows call
- Final AddRoundKey call
The number of rounds that are used and the size of the expanded key, EK, are dependent on the size of the provided key. The following table shows the correlation between the key length, the number of rounds, and the length of the expanded key:
| Key Length (Bits) | Number of Rounds | Expanded Key Length (Words) |
|---|---|---|
| 128 | 10 | 44 |
| 192 | 12 | 72 |
| 256 | 14 | 112 |
Example code for AES might look like the following:
def cipher(self, pt):
"""Basic AES implementation.
Args:
pt (bytes): Plaintext to encrypt
Returns:
list: Encrypted Ciphertext formatted as list of bytes
"""
state = self.rows_to_columns(pt)
self.add_round_key(state, self.ek[0:4]) #ek is the expanded key
for round in range(1, 10):
self.sub_bytes(state)
self.shift_rows(state)
self.mix_columns(state)
self.add_round_key(state, self.ek[round*4:(round*4)+4])
self.sub_bytes(state)
self.shift_rows(state)
self.add_round_key(state, self.ek[-4:])
return state
State
The state for the traditional AES algorithm is depicted as a 4x4 matrix to which the plaintext block is mapped. The block is copied to this matrix row by row; meaning that the first byte will be in column one, row one and the second byte will be in column one, row two. This can be seen in the following image where P denotes the plaintext array and Px denotes the byte at index x of the plaintext array:
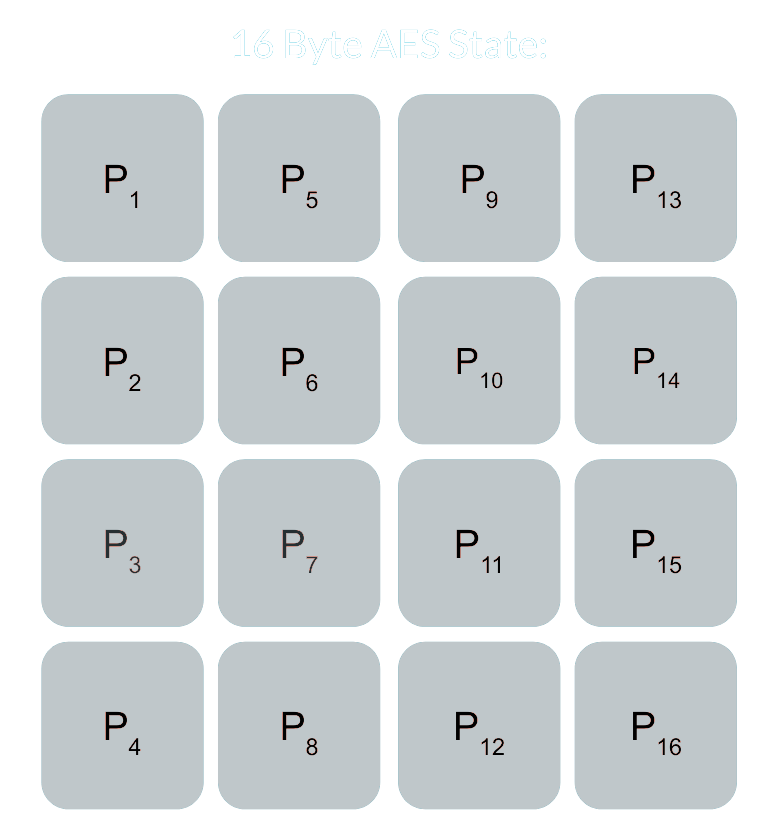 Basic AES State
Basic AES State
Key Expansion
The expanded key for AES is a list of four-byte words that are derived from the original key. The first words in the array are the same as the original key. For example, the first four bytes in the key array would be the first word in the expanded key, EK, like so:
key = [0x00, 0x11, 0x22, 0x33, 0x44, 0x55, 0x66, 0x77, 0x88, 0x99, 0xaa, 0xbb, 0xcc, 0xdd, 0xee, 0xff]
expanded_key = [0x00112233,
0x44556677,
0x8899aabb,
0xccddeeff,
...]
Each additional word is the result of XORing the previous word by the word at index i - NK where i is the current index and NK is the number of four-byte words that are in the original cipher key (4, 6, or 8 depending on the number of bits in the key). When the current index is a multiple of NK, the previous word is transformed before undergoing the XOR. This consists of the word being rotated to the left by one (i.e 0xAABBCCDD becomes 0xBBCCDDAA), then each byte being substituted by a value in AES’s Substitution Box (S-Box)– a 256 byte array. This new four-byte word is then XORed by a “round constant”, RCON. The round constant, RCON, can be computed from the algorithm: 2i-1 << 24 which, however, uses a Galois Field to perform multiplication instead of normal Base-10 multiplication. This type of multiplication is beyond the scope of this article, but you can read more about it here. The round constants can also be hardcoded in with the following values for the standard AES-128 algorithm:
| Index | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Values | None | 0x01 | 0x02 | 0x04 | 0x08 | 0x10 | 0x20 | 0x40 | 0x80 | 0x1B | 0x36 |
The entire AES-128 key expansion algorithm could look like the following Python code:
# Round Constants
RCON = [None, 0x01, 0x02, 0x04, 0x08, 0x10, 0x20, 0x40, 0x80, 0x1B, 0x36]
def subword(self, word):
"""AES SubWord Method.
Args:
word (list): Word to transform
Returns:
int: Transformed word
"""
bs = struct.pack('>I', word)
nw = []
for b in bs:
nw.append(self.SBOX[b])
nw = struct.unpack('>I', bytes(nw))[0]
return nw
def rotword(self, word):
"""AES RotateWord Method.
Args:
word (list): Word to transform
Returns:
int: Transformed word
"""
bs = list(struct.pack('>I', word))
bs.append(bs.pop(0))
nw = struct.unpack('>I', bytes(bs))[0]
return nw
def key_expansion(self, key):
"""AES Key Expansion Algorithm.
Args:
key (bytes): Key to expand
Returns:
list: List of words for expanded key
"""
ek = []
i = 0
while i < 4:
b = bytes(key[i*4:(i*4)+4])
w = struct.unpack('>I', b)[0]
ek.append(w)
i += 1
while i < 44: # 44 is the number of words in the expanded key
tmp = ek[i-1]
if i % 4 == 0: # Hardcoding the NK value "4" to be AES-128 specific
rcon_val = struct.unpack('>I',
bytes([self.RCON[i//4], 0, 0, 0]))[0]
tmp = self.subword(self.rotword(tmp)) ^ rcon_val
nw = tmp ^ ek[i-4]
ek.append(nw)
i += 1
return ek
Substitution Box (S-Box)
The AES S-Box is a 256-byte hardcoded array. This array is used for the SubWord function in the Key Expansion algorithm, as well as the SubByte function in the main cipher. The bytes in the S-Box are as follows:
| 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 0x63 | 0x7C | 0x77 | 0x7B | 0xF2 | 0x6B | 0x6F | 0xC5 | 0x30 | 0x01 | 0x67 | 0x2B | 0xFE | 0xD7 | 0xAB | 0x76 |
| 0xCA | 0x82 | 0xC9 | 0x7D | 0xFA | 0x59 | 0x47 | 0xF0 | 0xAD | 0xD4 | 0xA2 | 0xAF | 0x9C | 0xA4 | 0x72 | 0xC0 |
| 0xB7 | 0xFD | 0x93 | 0x26 | 0x36 | 0x3F | 0xF7 | 0xCC | 0x34 | 0xA5 | 0xE5 | 0xF1 | 0x71 | 0xD8 | 0x31 | 0x15 |
| 0x04 | 0xC7 | 0x23 | 0xC3 | 0x18 | 0x96 | 0x05 | 0x9A | 0x07 | 0x12 | 0x80 | 0xE2 | 0xEB | 0x27 | 0xB2 | 0x75 |
| 0x09 | 0x83 | 0x2C | 0x1A | 0x1B | 0x6E | 0x5A | 0xA0 | 0x52 | 0x3B | 0xD6 | 0xB3 | 0x29 | 0xE3 | 0x2F | 0x84 |
| 0x53 | 0xD1 | 0x00 | 0xED | 0x20 | 0xFC | 0xB1 | 0x5B | 0x6A | 0xCB | 0xBE | 0x39 | 0x4A | 0x4C | 0x58 | 0xCF |
| 0xD0 | 0xEF | 0xAA | 0xFB | 0x43 | 0x4D | 0x33 | 0x85 | 0x45 | 0xF9 | 0x02 | 0x7F | 0x50 | 0x3C | 0x9F | 0xA8 |
| 0x51 | 0xA3 | 0x40 | 0x8F | 0x92 | 0x9D | 0x38 | 0xF5 | 0xBC | 0xB6 | 0xDA | 0x21 | 0x10 | 0xFF | 0xF3 | 0xD2 |
| 0xCD | 0x0C | 0x13 | 0xEC | 0x5F | 0x97 | 0x44 | 0x17 | 0xC4 | 0xA7 | 0x7E | 0x3D | 0x64 | 0x5D | 0x19 | 0x73 |
| 0x60 | 0x81 | 0x4F | 0xDC | 0x22 | 0x2A | 0x90 | 0x88 | 0x46 | 0xEE | 0xB8 | 0x14 | 0xDE | 0x5E | 0x0B | 0xDB |
| 0xE0 | 0x32 | 0x3A | 0x0A | 0x49 | 0x06 | 0x24 | 0x5C | 0xC2 | 0xD3 | 0xAC | 0x62 | 0x91 | 0x95 | 0xE4 | 0x79 |
| 0xE7 | 0xC8 | 0x37 | 0x6D | 0x8D | 0xD5 | 0x4E | 0xA9 | 0x6C | 0x56 | 0xF4 | 0xEA | 0x65 | 0x7A | 0xAE | 0x08 |
| 0xBA | 0x78 | 0x25 | 0x2E | 0x1C | 0xA6 | 0xB4 | 0xC6 | 0xE8 | 0xDD | 0x74 | 0x1F | 0x4B | 0xBD | 0x8B | 0x8A |
| 0x70 | 0x3E | 0xB5 | 0x66 | 0x48 | 0x03 | 0xF6 | 0x0E | 0x61 | 0x35 | 0x57 | 0xB9 | 0x86 | 0xC1 | 0x1D | 0x9E |
| 0xE1 | 0xF8 | 0x98 | 0x11 | 0x69 | 0xD9 | 0x8E | 0x94 | 0x9B | 0x1E | 0x87 | 0xE9 | 0xCE | 0x55 | 0x28 | 0xDF |
| 0x8C | 0xA1 | 0x89 | 0x0D | 0xBF | 0xE6 | 0x42 | 0x68 | 0x41 | 0x99 | 0x2D | 0x0F | 0xB0 | 0x54 | 0xBB | 0x16 |
SubBytes
The SubBytes function in AES will replace each byte in the state with a byte in the Substitution Box at the index Pi. The following graphic represents this exchange:
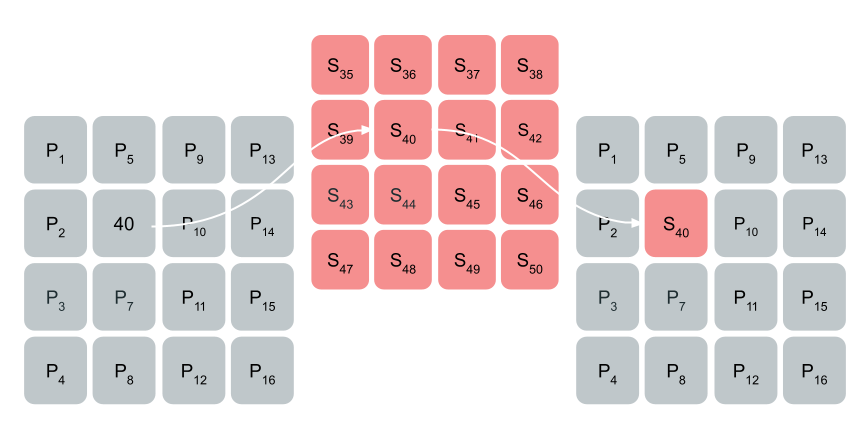 Substituting byte “40” in the state with the byte at index 40 in the S-Box
Substituting byte “40” in the state with the byte at index 40 in the S-Box
The code for this function could look like the following:
def sub_bytes(self, state):
"""AES SubBytes Method.
Args:
state (list): AES State
"""
for i in range(len(state)):
state[i] = self.SBOX[state[i]]
ShiftRows
The ShiftRows function will rotate each row in the state to the left. The first row is not shifted at all, the second row is shifted by one, the third row by two, and the fourth row by three.
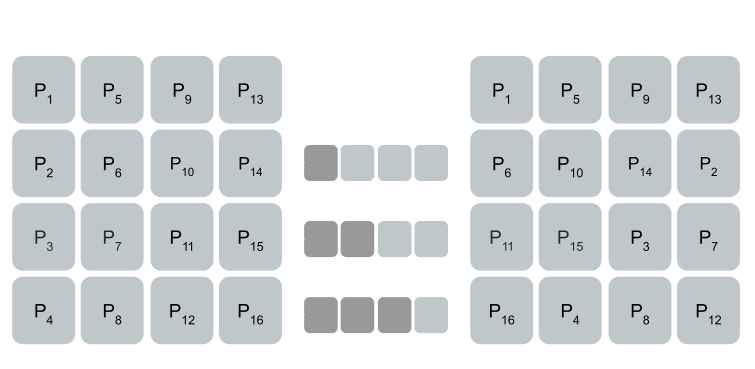 AES ShiftRows Function
AES ShiftRows Function
The code for the ShiftRows function can be:
def shift_rows(self, state):
"""AES ShiftRows Method.
Args:
state (list): AES State
"""
for i in range(1, 4):
state[i*4:(i*4)+4] = state[(i*4)+i:(i*4)+4] + state[(i*4):(i*4)+i]
MixColumns
MixColumns will perform matrix multiplication on each column in the state. The multiplication here also uses the Galois field like in the Key Expansion function. I managed to find a pure Python implementation of this algorithm in GitHub from the user lovasoa which looks like the following:
def gmul(a, b):
"""Special AES function used for multiplication
Args:
a (int): Integer to multiply
b (int): Integer to multiply
Returns:
int: The product of the values
"""
p = 0
for c in range(8):
if b & 1:
p ^= a
a <<= 1
if a & 0x100:
a ^= 0x11b
b >>= 1
return p
The Matrix multiplication looks like the following:
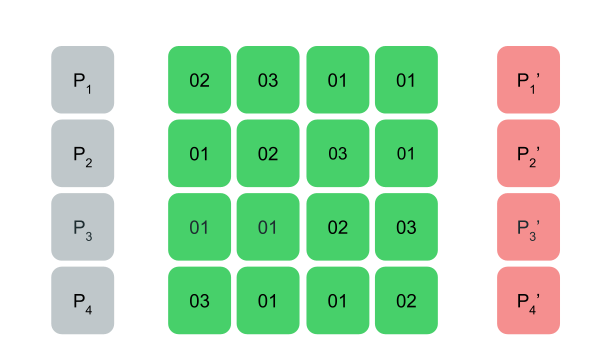 AES MixColumns Function
AES MixColumns Function
The entire function can be shown as the following Python code:
def mix_columns(self, state):
"""AES MixColumns Method.
Args:
state (list): AES State
"""
for i in range(4):
a = state[i]
b = state[i+4]
c = state[i+8]
d = state[i+12]
state[i] = gmul(2, a) ^ gmul(3, b) ^ c ^ d
state[i+4] = a ^ gmul(2, b) ^ gmul(3, c) ^ d
state[i+8] = a ^ b ^ gmul(2, c) ^ gmul(3, d)
state[i+12] = gmul(3, a) ^ b ^ c ^ gmul(2, d)
AddRoundKey
The AddRoundKey function in AES will XOR part of the expanded key by each column of the state. This can be shown as the following code:
def add_round_key(self, state, words):
"""AES AddRoundKey Method.
Args:
state (list): AES State
words (list): List of words from expanded key
"""
for i in range(len(words)):
wb = struct.pack('>I', words[i])
for j in range(4):
state[(j*4)+i] = state[(j*4)+i] ^ wb[j]
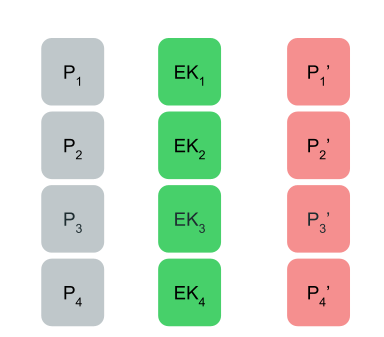 AddRoundKey Function
AddRoundKey Function
AES Lookup Table (T-Table) Method
To make the AES algorithm more efficient, the MixColumns, ShiftRows, and SubBytes functions were combined into a a single operation that utilizes five lookup tables. The key expansion algorithm is the same as the original AES algorithm and the state is treated as a normal array and not as a 4x4 matrix.
Lookup Table Generation
The first four lookup tables (T-Tables) are generated by multiplying each byte of the S-Box by the matrix used in the MixColumns function. This will create four tables containing 256 four-byte words. They can be generated using the following algorithm:
T1 = {S[i] * 2, S[i], S[i], S[i] * 3}
T2 = {S[i] * 3, S[i] * 2, S[i], S[i]}
T3 = {S[i], S[i] * 3, S[i] * 2, S[i]}
T4 = {S[i], S[i], S[i] * 3, S[i] * 2}
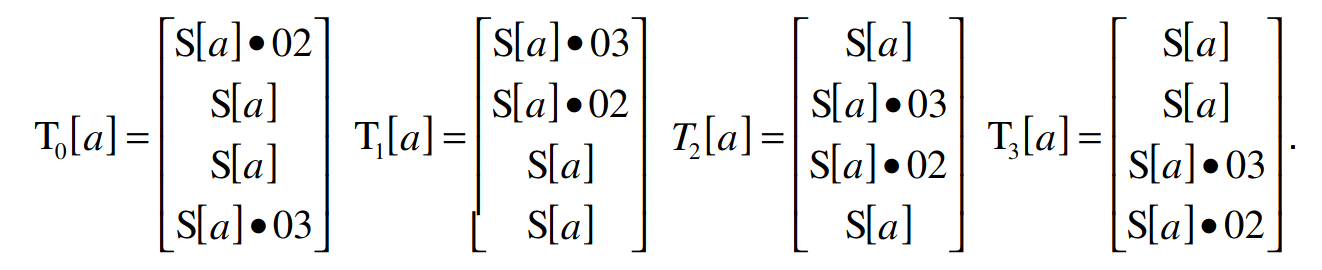 AES T-Table Generation
AES T-Table Generation
The final T-Table combines each byte of the S-Box into a four-byte word and is only used during the final round of encryption.
# Final T-Table generation
T5 = {S[i], S[i], S[i], S[i]}
The entire generation of the lookup tables can look like the following Python code:
def generate_t_tables(self):
"""Generates the tables used for the AES lookup table method."""
self.t1 = []
self.t2 = []
self.t3 = []
self.t4 = []
self.t5 = []
for i in range(len(self.SBOX)):
word1 = [gmul(self.SBOX[i], 2), self.SBOX[i],
self.SBOX[i], gmul(self.SBOX[i], 3)]
word2 = [gmul(self.SBOX[i], 3), gmul(self.SBOX[i], 2),
self.SBOX[i], self.SBOX[i]]
word3 = [self.SBOX[i], gmul(self.SBOX[i], 3),
gmul(self.SBOX[i], 2), self.SBOX[i]]
word4 = [self.SBOX[i], self.SBOX[i],
gmul(self.SBOX[i], 3), gmul(self.SBOX[i], 2)]
word5 = [self.SBOX[i]] * 4
self.t1.append(struct.unpack('>I', bytes(word1))[0])
self.t2.append(struct.unpack('>I', bytes(word2))[0])
self.t3.append(struct.unpack('>I', bytes(word3))[0])
self.t4.append(struct.unpack('>I', bytes(word4))[0])
self.t5.append(struct.unpack('>I', bytes(word5))[0])
Round Encryption
For each round of encryption, the AES T-Table algorithm will XOR a byte of the four lookup tables at the index of the original plaintext array. For example, a normal round would look like the following pseudo-code:
A[0] = PT[0:4] ^ W[0]
A[1] = PT[4:8] ^ W[1]
A[2] = PT[8:12] ^ W[2]
A[3] = PT[12:16] ^ W[3]
K = 4
for round in NUM_ROUNDS:
S[0:4] = A[0] # Convert word to bytes
S[4:8] = A[1]
S[8:12] = A[2]
S[12:16] = A[3]
A[0] = T1[S[0]] ^ T2[S[5]] ^ T3[S[10]] ^ T4[S[15]] ^ W[K+0]
A[1] = T1[S[4]] ^ T2[S[9]] ^ T3[S[14]] ^ T4[S[3]] ^ W[K+1]
A[2] = T1[S[8]] ^ T2[S[13]] ^ T3[S[2]] ^ T4[S[7]] ^ W[K+2]
A[3] = T1[S[12]] ^ T2[S[1]] ^ T3[S[6]] ^ T4[S[11]] ^ W[K+3]
This method is more efficient than calling the separate SubBytes, ShiftRows, and MixColumns functions because it is all done in one step. There is no need to peform multiple loops or function calls when all the methods are combined at once.
Final Round
The final round of encryption is similar to the normal rounds except it is using the fifth T-Table and each XOR gets appended to the ciphertext. The following pseudo-code demonstrates this process:
CT[0:4] = T5[S[0]] ^ T5[S[5]] ^ T5[S[10]] ^ T5[S[15]] ^ W[K+0]
CT[4:8] = T5[S[4]] ^ T5[S[9]] ^ T5[S[14]] ^ T5[S[3]] ^ W[K+1]
CT[8:12] = T5[S[8]] ^ T5[S[13]] ^ T5[S[2]] ^ T5[S[7]] ^ W[K+2]
CT[12:16] = T5[S[12]] ^ T5[S[1]] ^ T5[S[6]] ^ T5[S[11]] ^ W[K+3]
AES T-Table Python Code
The full code for the AES T-Table implementation could look like the following:
def cipher_t_table(self, pt):
"""Lookup Table AES implementation.
Args:
pt (bytes): Plaintext to encrypt
Returns:
bytes: Encrypted Ciphertext
"""
ct = []
a = [0, 0, 0, 0]
# t is a temporary array to avoid us changing array a while performing the algorithm
t = [0, 0, 0, 0]
a[0] = struct.unpack('>I', pt[0:4])[0] ^ self.ek[0]
a[1] = struct.unpack('>I', pt[4:8])[0] ^ self.ek[1]
a[2] = struct.unpack('>I', pt[8:12])[0] ^ self.ek[2]
a[3] = struct.unpack('>I', pt[12:16])[0] ^ self.ek[3]
print(a)
for round in range(1, 10):
for i in range(4):
# Using binary rotation instead of splitting words into array
t[i] = (self.t1[(a[i] >> 24) & 0xff] ^
self.t2[(a[(i + 1) % 4] >> 16) & 0xff] ^
self.t3[(a[(i + 2) % 4] >> 8) & 0xff] ^
self.t4[(a[(i + 3) % 4]) & 0xff] ^
self.ek[(round*4)+i])
a = t.copy()
# Final round of encryption
for i in range(4):
ct.append(self.SBOX[(a[i] >> 24) & 0xff] ^
((self.ek[-4+i] >> 24) & 0xff))
ct.append(self.SBOX[(a[(i + 1) % 4] >> 16) & 0xff] ^
((self.ek[-4+i] >> 16) & 0xff))
ct.append(self.SBOX[(a[(i + 2) % 4] >> 8) & 0xff] ^
((self.ek[-4+i] >> 8) & 0xff))
ct.append(self.SBOX[(a[(i + 3) % 4]) & 0xff] ^
((self.ek[-4+i]) & 0xff))
return bytes(ct)
Identifying AES in Assembly Code
Identifying the S-Box/T-Tables
A quick win when trying to identify if a binary is using AES is to look for either the Substitution Box or any of the lookup tables from the T-Tables implementation. For example, in my previous post on sodinokibi ransomware, it was found that the sample was utilizing AES to encrypt data. We can search for the first word of one of the T-Tables in Cutter and see that it exists in the binary.
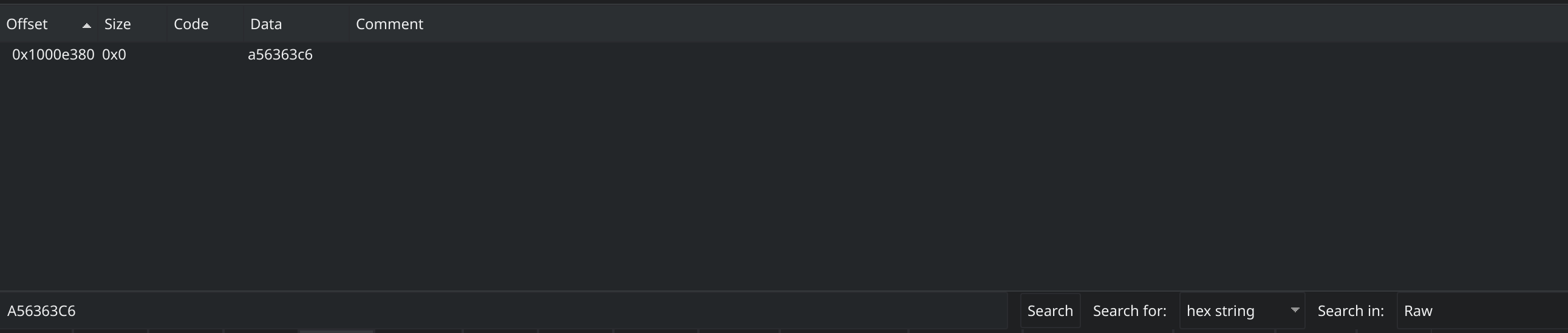 Searching for word in T-Table in Cutter
Searching for word in T-Table in Cutter
Now if we go to that location we can confirm that this is one of the T-Tables used by AES.
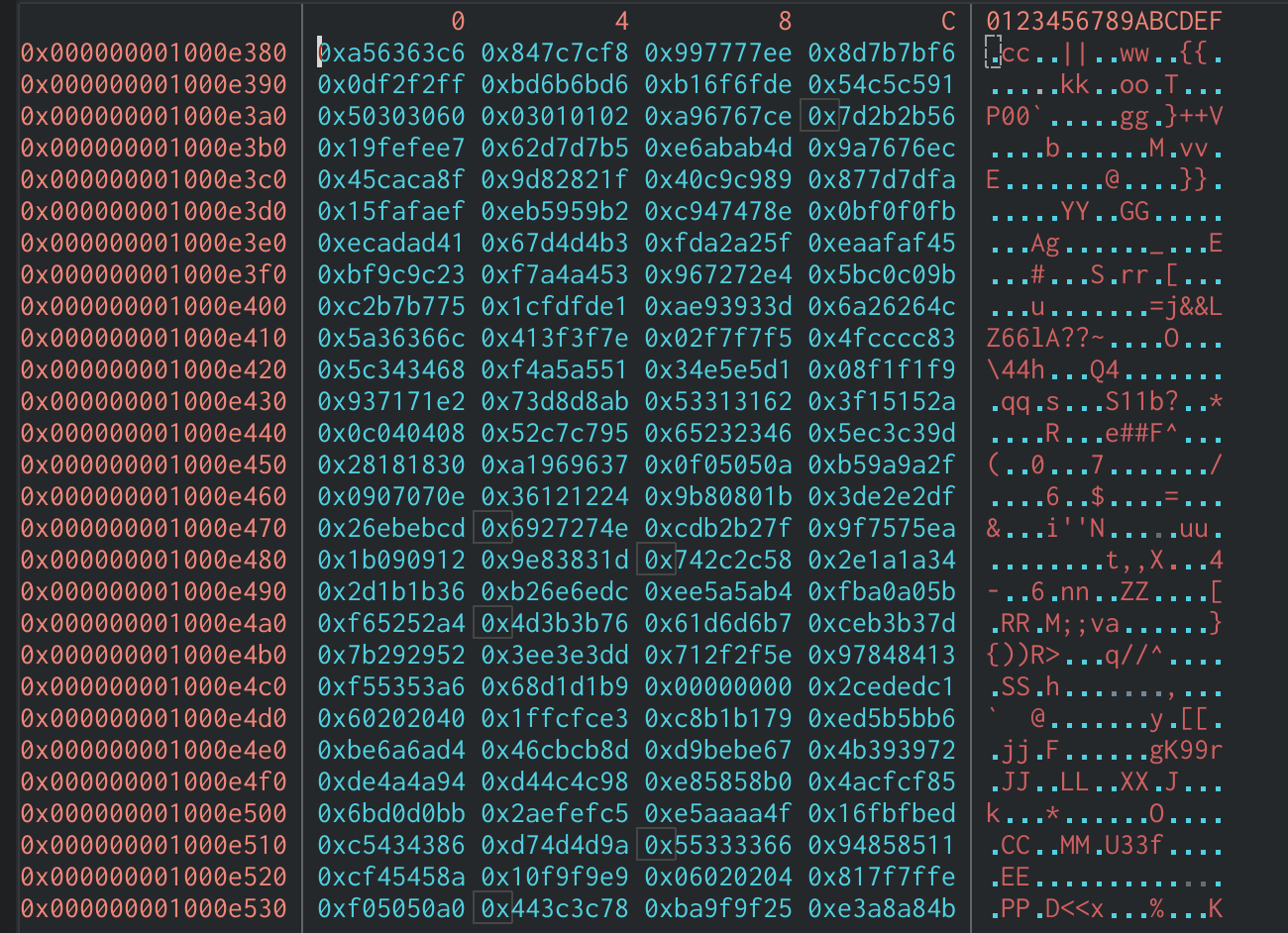 Hexdump of T-Table in Cutter
Hexdump of T-Table in Cutter
This is a great indicator to identify AES. If we search for references to this array in Cutter, we will see one of the XOR operations during a round of encryption which confirms the use of AES.
 T-Table XOR Assembly Code
T-Table XOR Assembly Code
Identifying Normal AES Functions
Another way to tell if AES is being used is to identify the individual ShiftRows, SubBytes, MixColumns, and AddRoundKey functions. Breaking down and identifying each function individually is more efficient than reverse engineering a large amount of code at once. We will be using the GitHub project tiny-AES, a pure implementation of the AES algorithm using C code, as an example to show how the code would look in Assembly.
AddRoundKey in Assembly
The AddRoundKey function in this binary takes three arguments. The first argument is shifted left by four then AND’d by 0xff0 which is the same as multiplying it by 16, the same size as the state. This is a good indicator that this argument will hold the current round number. This value is then added to the third argument of the function. Because the state cannot be more than 16 bytes in length, we can assume that the third argument is the expanded key and the second argument is the state. After this, we can see two loops that will XOR the state column-by-column against the expanded key.
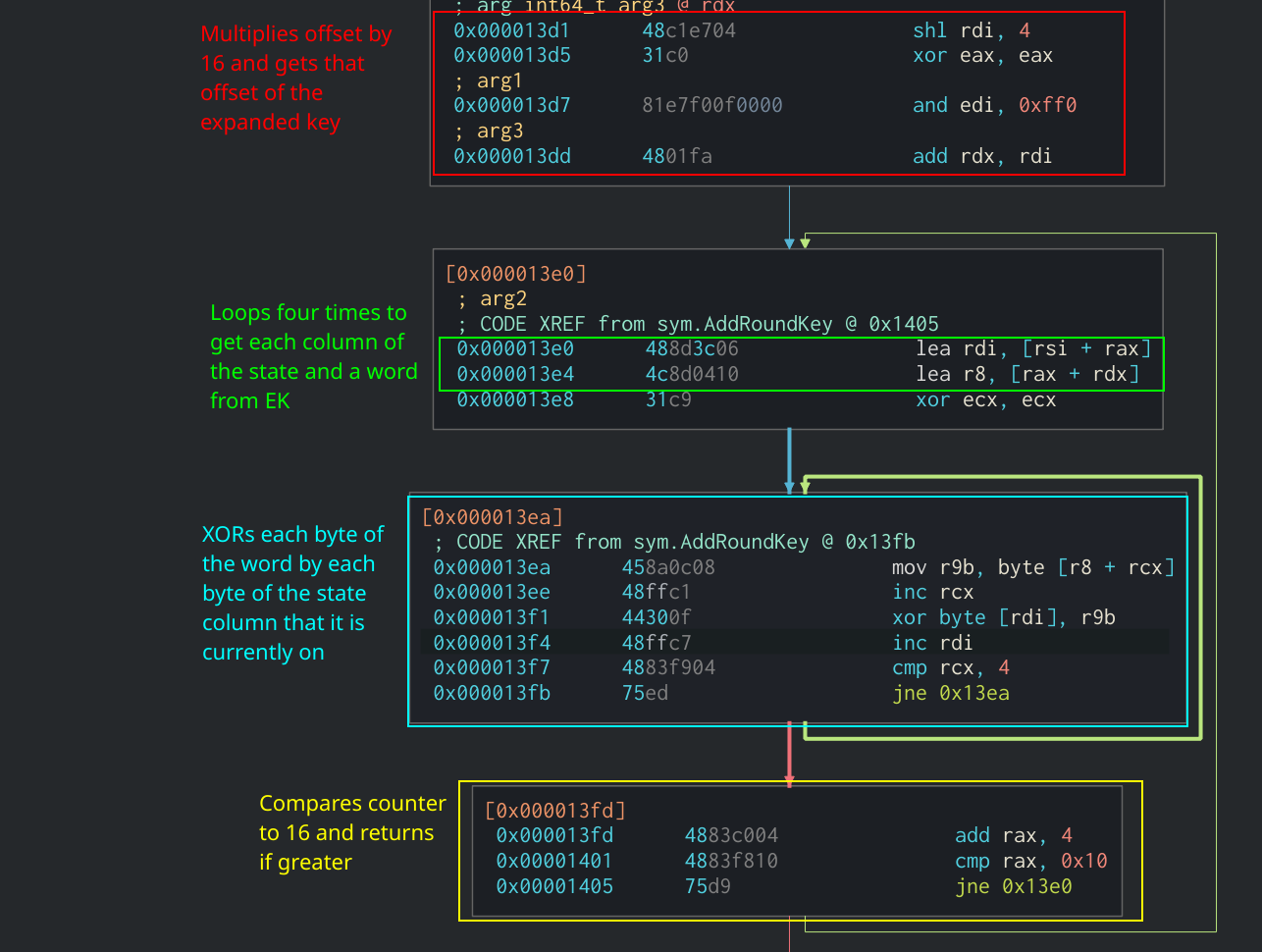 AddRoundKey Function in Assembly
AddRoundKey Function in Assembly
SubBytes in Assembly
When compiling the code from the GitHub project, the SubBytes is added in-line in the main cipher function rather than making a function call. We are able to identify it as SubBytes by the fact that it takes each byte of the state and uses it as an offset in the S-Box array. Then it will take the byte at that offest and put it into the state at the current index. We can see all of this being done in two loops in the Cipher function:
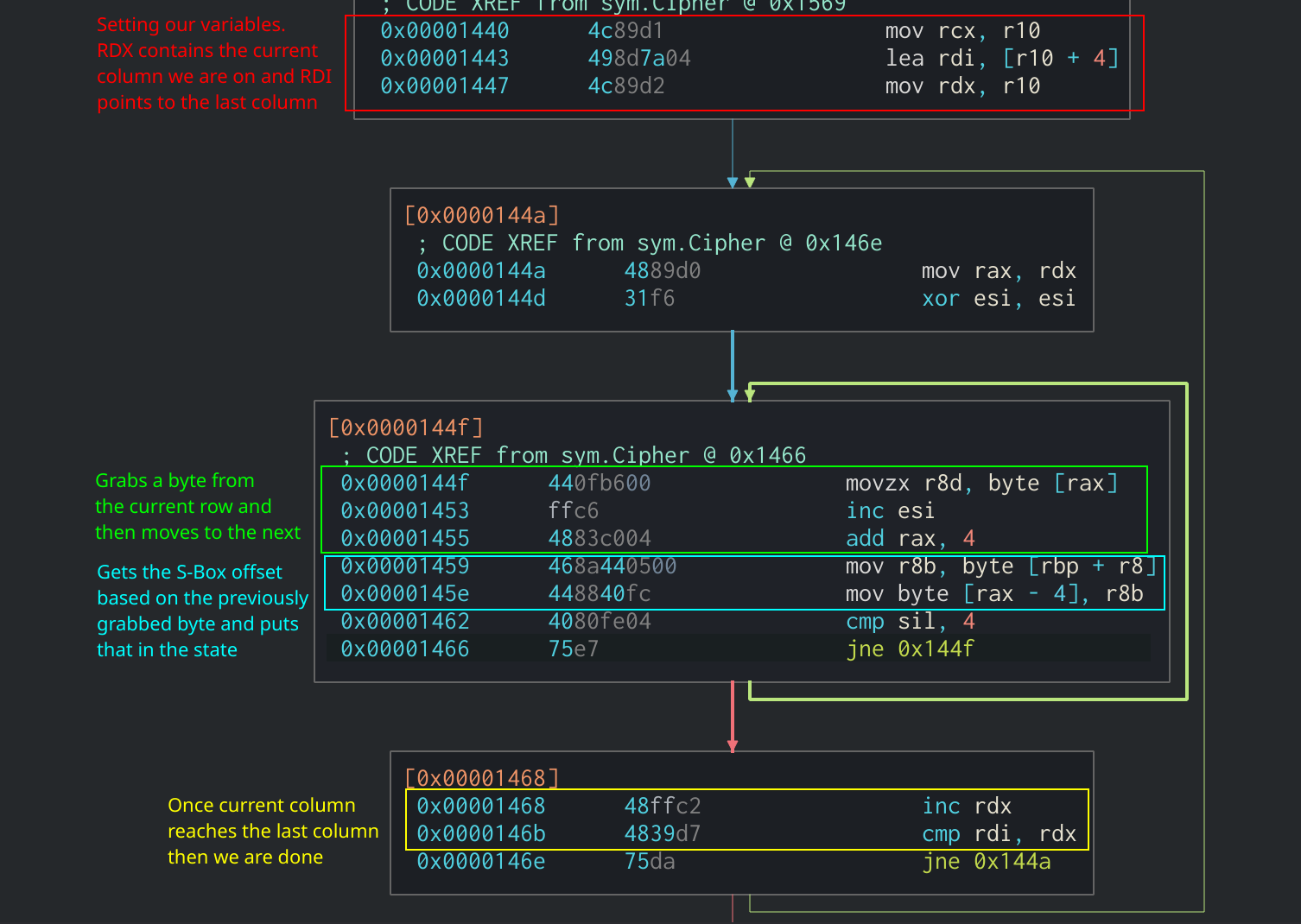 SubBytes function in Assembly
SubBytes function in Assembly
ShiftRows in Assembly
The ShiftRows function is also added in-line in the main cipher function. It is pretty easy to spot as it consists of several mov instructions on the state to shift each row the correct amount of times.
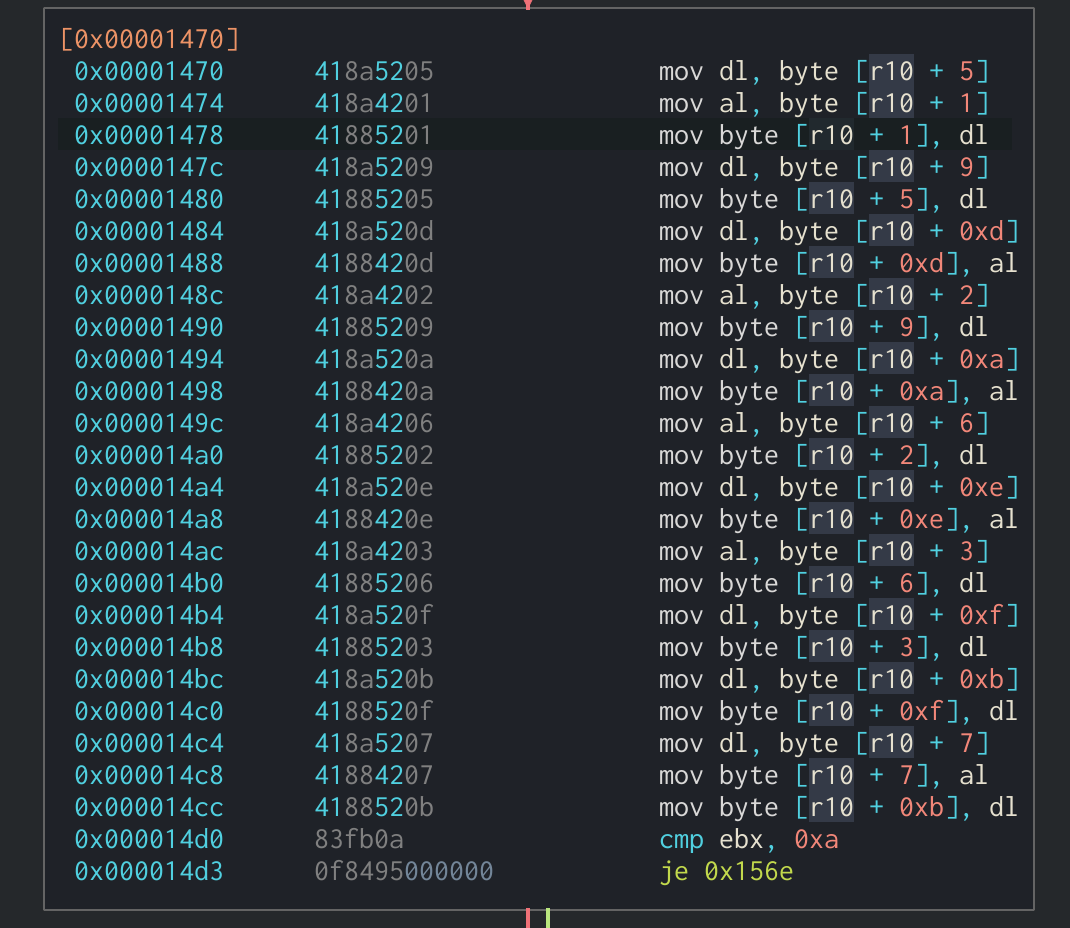 ShiftRows function in Assembly
ShiftRows function in Assembly
MixColumns in Assembly
Finally, the MixColumns function is also in-line. It can be identified through multiple XOR operations being done on the state along with the Galois Field multiplication function. The results of the XOR operations are then put back into the state. In this binary, the MixColumns function will loop four times and perform the XOR operations on each row’s values then update that row with the new values. This can all be seen in the following section:
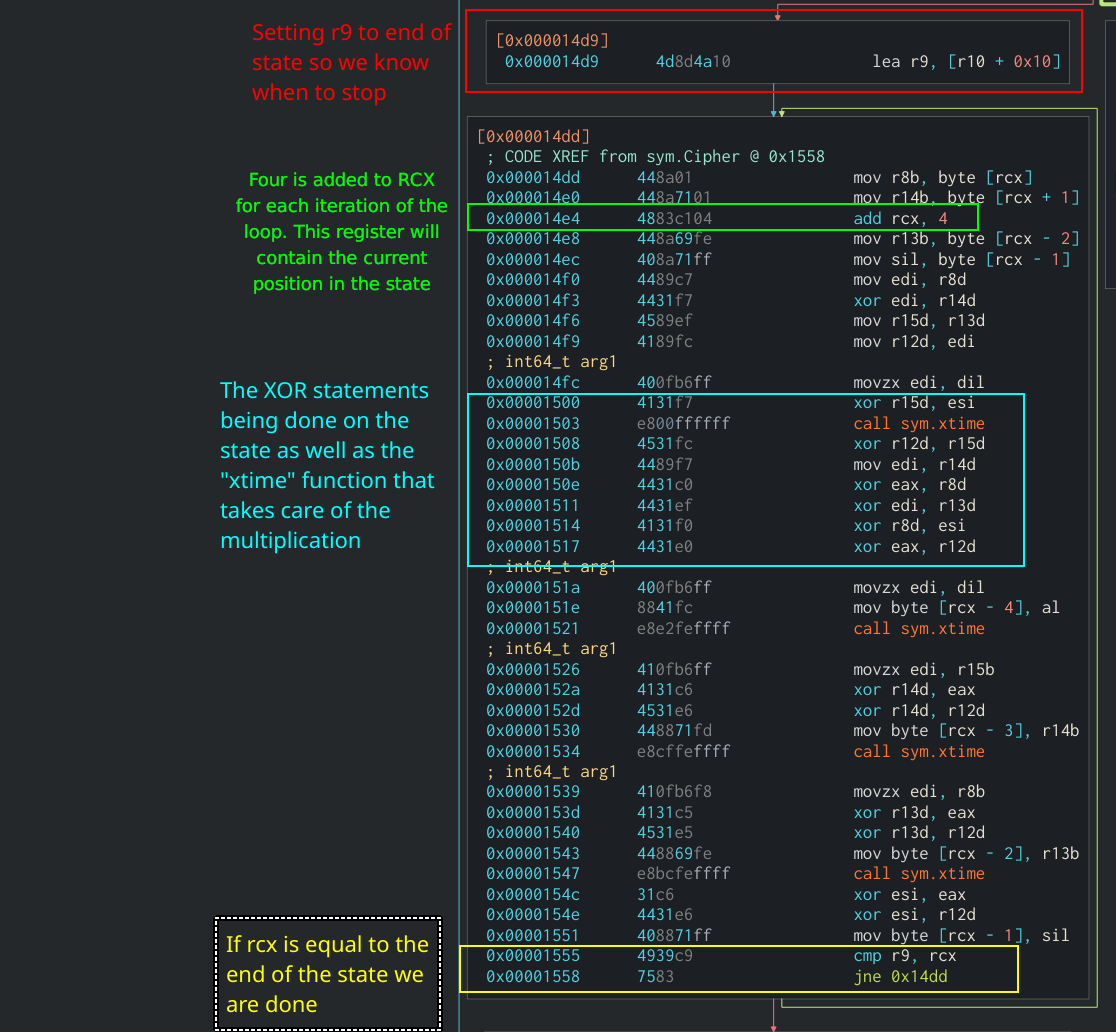 MixColumns in Assembly
MixColumns in Assembly
Identifying Key Expansion
Since the Key Expansion algorithm is the same between the T-Table and normal implementations of AES, this indicator can be used to identify AES in other binaries. The first part of the Key Expansion algorithm copies the first four words of the original key into the expanded key. In Assembly, this would look like several mov instructions moving a byte of the original key into the new expanded key. This example is from the tiny-AES GitHub project mentioned earlier:
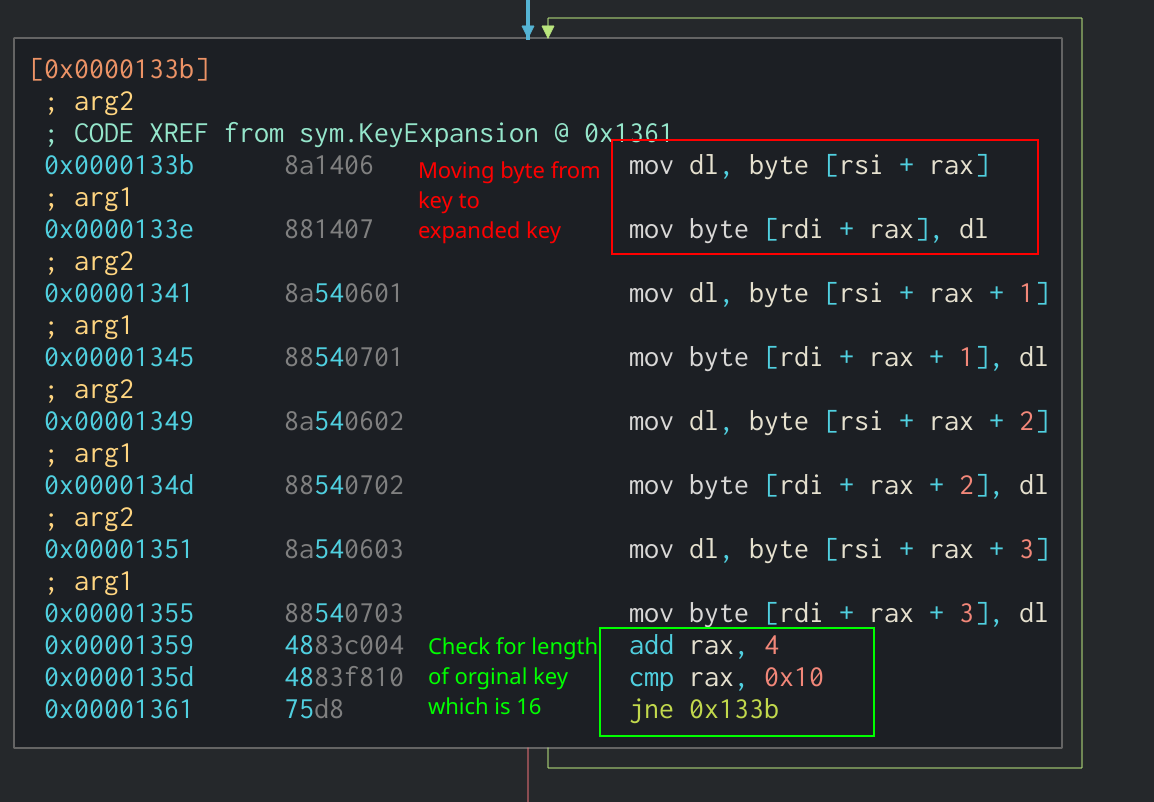 First part of Key Expansion algorithm in Assembly
First part of Key Expansion algorithm in Assembly
The next part of the Key Expansion algorithm checks to see if the current index is divisible by four. If it is, the application will split the previous word into separate registers and performs a lookup of each one in the S-Box (r9). Afterwards, it rotates each byte individually to a new register. This is an in-line implementation of the SubWord and RotWord functions that were described earlier in the article. Finally, the most significant byte of the new word is XOR’d by one of the Round Constants stored in r10.
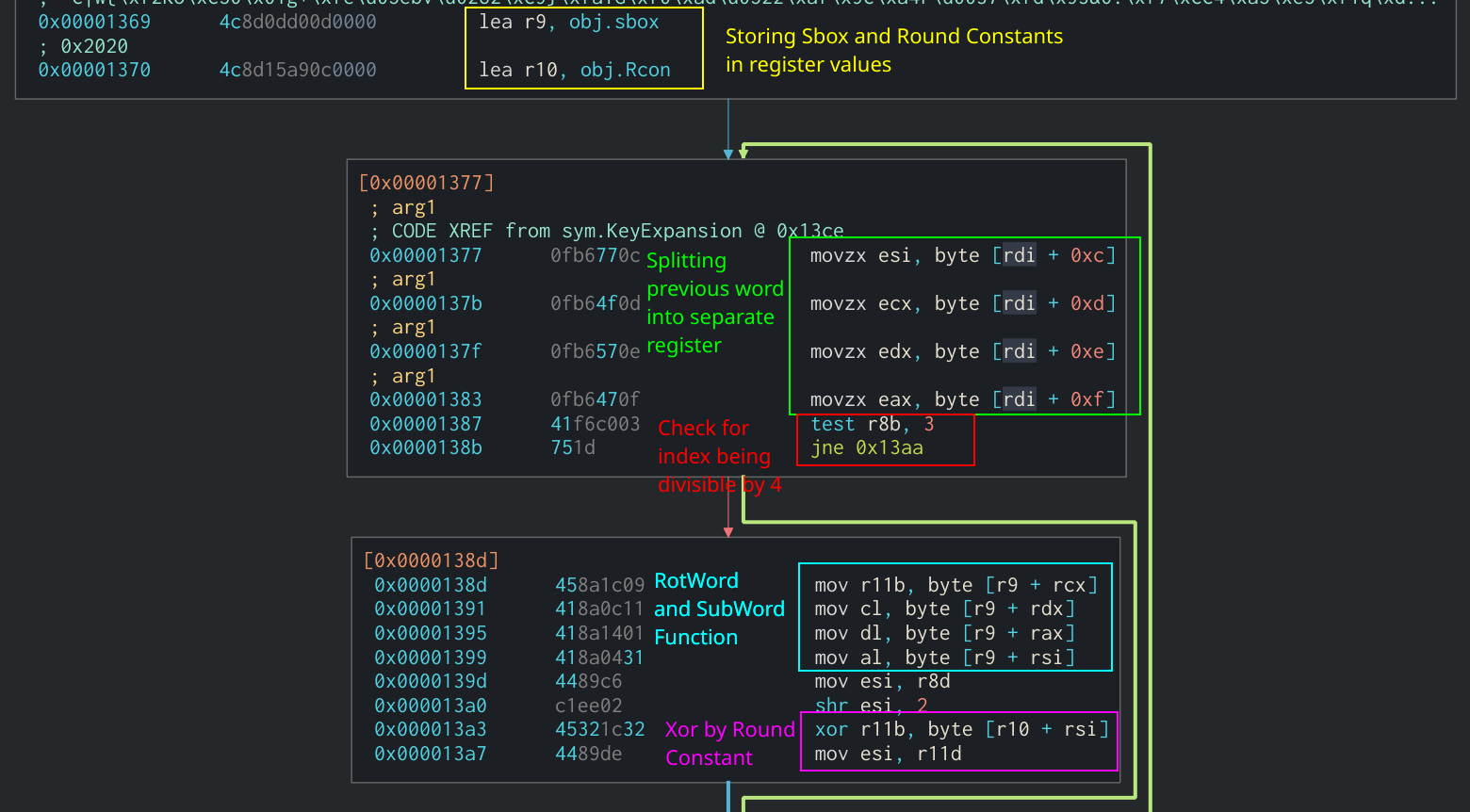 RotWord, SubWord, and Round Constant use in Assembly
RotWord, SubWord, and Round Constant use in Assembly
We can see in the Assembly that the new word is being XOR’d by the word four indices previous in the expanded key.
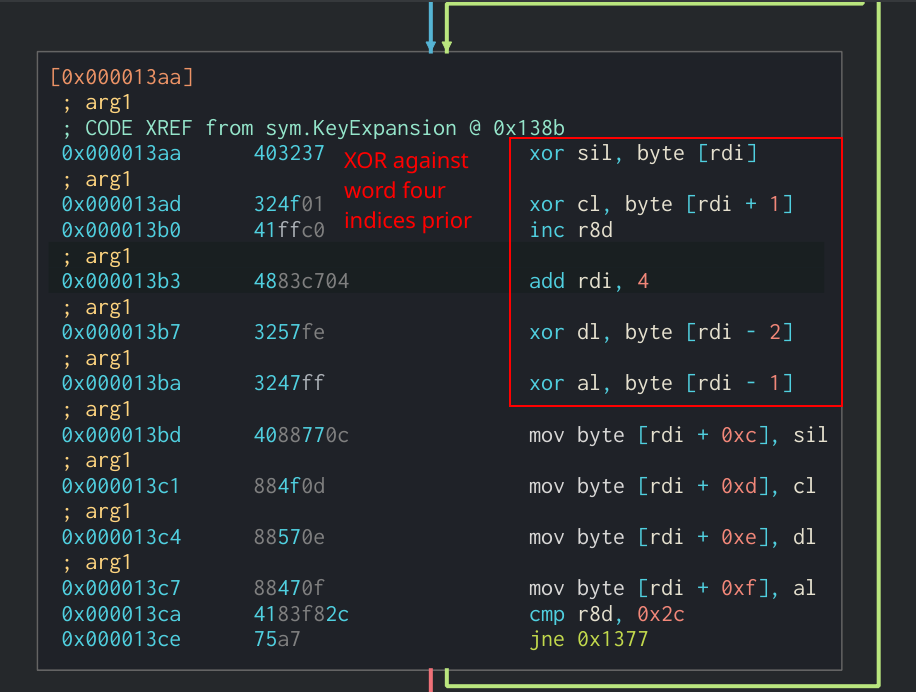 Final section of Key Expansion algorithm
Final section of Key Expansion algorithm
Conclusion
Hopefully this article can help analysts identify implementations of the AES algorithm in other binaries. For additional reading into some of the design decisions for AES and more info on the mathematics behind it, I recommend reading two of the official NIST documentations on AES:
- Federal Information Processing Standards Publication 197, Advanced Encryption Standard (AES)
- AES Proposal: Rijndael
If you have any questions or comments about this post, feel free to message me on my Twitter or LinkedIn. I hope to do more posts like this in the future.
Thanks for reading and happy reversing!






